|
El armonioso frontal del
Partenón está inscrito en un rectángulo que tiene la
propiedad de que el cociente de sus lados vale
 (llamado número áureo)
(llamado número áureo)

Construcción de un
rectángulo áureo a partir de un cuadrado

Esta proporción también se halla
en el cuerpo humano: el alemán Zeysing efectuó medidas
sobre miles de personas y llegó a la conclusión de que en las
estatuas antiguas y en los hombres perfectamente proporcionados
(modelos, matemáticos, etc.) el ombligo divide su altura total
según la sección áurea. La citada proporción está en las
medidas de las tarjetas de crédito, se halla presente en el
perfil de muchos huevos (relación entre sus ejes) y en otros
muchos ejemplos de la arquitectura y la naturaleza. se da el
caso curioso de que Fechner, el inventor de la psicología
física, pidió a numerosas personas que eligieran, de entre
varios rectángulos diferentes (comprendiendo el cuadrado), aquél
cuya forma más le agradase y el rectángulo áureo obtuvo una
acentuada mayoría.



Es el número del arte por
excelencia, y quizá, de todos los artistas que lo han empleado a
lo largo de la historia, sea Leonardo da Vinci el artista que
jugó de manera más atractiva con el número áureo, algo muy
acorde con su carácter tendente a los enigmas. Un buen ejemplo
de ello es su famoso Hombre de Vitrubio, donde la relación
existente entre las partes se corresponde con esta medida,
siguiendo los planteamientos de simetría enunciados por este
arquitecto y tratadista romano. No es el único: los templos
griegos, algunas obras de arte povera, la famosa Leda atómica de
Dalí, el Apolo de Belvedere, El Escorial en Madrid, la Venus de
Botticelli, e, incluso se ha llegado a considerar, las pirámides
de Gizeh, fueron realizados, en ocasiones de forma inconsciente,
siguiendo una proporción áurea, algo que no es apreciable a
primera vista pero que confiere a estas creaciones una
apariencia armónica distinguible pero difícil de explicar.
¿Sabías que...
El número aúreo es el único que
cumple que Φ2=Φ+1 ?

- El número e
(2,7182818284590452354...)
Este número se usa en el
crecimiento exponencial

El número e, base de los
logaritmos naturales o neperianos, es sin duda el número más
importante del campo del cálculo. Como e es un número
trascendental, y por lo tanto es irracional, su valor no puede
ser dado exactamente como un número finito o con decimales
periódicos.
Sirve entre otras cosas para calcular valores de crecimiento
continuo como por ejemplo la población dentro de unos años, el
volumen de un árbol dentro de cierto tiempo, etc.

-
El número π
(3,14159265...)
Es un número
irracional que se usa en:
En geometría
- Longitud de
la circunferencia de radio r: C = 2 π
r
Áreas de secciones
cónicas:
- Área del
círculo de radio r: A = π r²
- Área de la
elipse con semiejes a y b: A =
π ab
Áreas de cuerpos
de revolución:
- Área del
cilindro: 2 π r (r+h)
- Área del
cono: π r² + π r g
- Área de la
esfera: 4 π r²
Volúmenes de
cuerpos de revolución:
- Volumen de la
esfera de radio r: V = (4/3) π r³
- Volumen de un
cilindro recto de radio r y altura
h: V = π r² h
- Volumen de un
cono recto de radio r y altura h:
V = π r² h / 3
Ecuaciones
expresadas en radianes:
- Ángulos: 180
grados son equivalentes a π radianes.
En estadística
- La
probabilidad de que dos enteros positivos
escogidos al azar sean primos entre sí es:
6/π²
- Si se eligen
al azar dos números positivos menores que 1,
la probabilidad de que junto con el número 1
puedan ser los lados de un triángulo
obtusángulo es: (π-2)/4
- El número
medio de formas de escribir un entero
positivo como suma de dos cuadrados
perfectos es π/4 (el orden es relevante).
- Aguja de
Buffon: si lanzamos al azar una aguja de
longitud L sobre una superficie en la que
hay dibujadas líneas paralelas separadas una
distancia D, la probabilidad de que la aguja
corte a una línea es: Dπ/2L
En análisis matemático,
algunas aproximaciones a π.
-
-

-
-
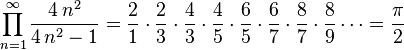
-
-
-
-
|